The Birthday Paradox
‘The Birthday Paradox’ is quite interesting and even surprising at first. Consider your’s and one of your friend’s classroom (assuming your friend is in another class). Let’s assume these two classes have 50 people in total. Would you expect any two people to share a birthday? You presumably said ‘no’, unless you have heard of this paradox before.
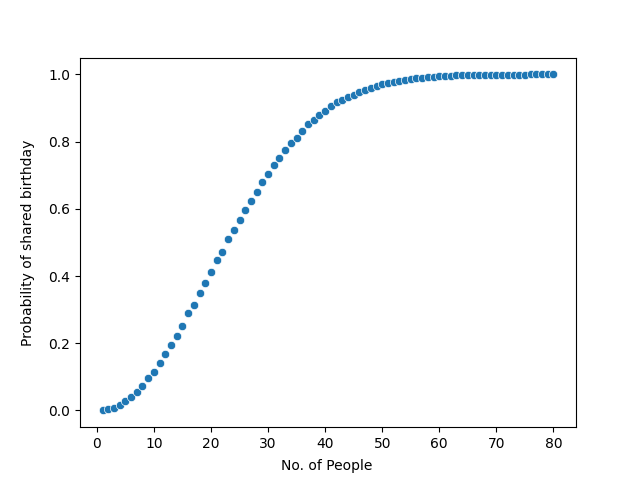
However, the chance of two people sharing a birthday in this setting would be extremely high. In fact, even if there are just about 23 people, there is a 50% chance that two people share a birthday. I simulated this problem in Python to create a cool curve. First, using a random number generator (RNG), a number between 1 and 365 (representing the birthday) was generated n number of times. Here, n would be the number of people (for my experiments, the n values range from 1 to 80). Then, this was simulated a bunch of times for each value of n to calculate the probability of a shared birthday. Below is the graph showing the probabilities at each n value.
From the graph above, we observe that, when there are 23 people in a room, the chance of a birthday pair is just above 50%. When there are 40 people, it’s a surprising 90%. This means that, if there are a 1000 rooms, each consisting of just 40 people, there would be a birthday pair in about 900 of those rooms. When the number of people in a setting exceeds 55, there is a near 100% chance of finding a birthday pair.
Normally, we would think that it’s quite surprising to find a birthday pair in a group of 25 or 30 people. Although, it would be more surprising if we don’t find one. If this, at first, stupefies you and seems like it all doesn’t make sense, don’t worry, I am with you. Sometimes, contemplating probability theory is tough.
Learn more
Anyway, if you find the birthday paradox interesting and would like to explore more into it, I recommend reading the first chapter of ‘Ten Great Ideas About Chance’ by Persi Diaconis & Brian Skyrms. It goes more into depth about this problem and introduces some equations which would aid your understanding.